Wh / V =
0.00 Ah
Conversion formula: Ah = Wh / V
What Is a Watt-Hour?
Watt-hours is a unit that measures how much energy an electrical system generates or consumes due to a given amount of power over a certain period (in hours). We could also say watt-hours is the amount of electrical power an electrical system consumes or produces in one hour.
Going by the definitions, one watt-hour is the amount of energy generated or consumed when one watt is generated or consumed in one hour.
While watt-hours is typically a unit for electrical energy consumption, it may also be used to define battery capacity. This is especially true for large batteries.
When a battery’s capacity is specified in watt-hours, that value represents how much energy the battery can store/supply. Basically, watt-hours is a battery’s energy capacity.
What Is an Amp-Hour?
Amp-hours is a unit that measures the amount of charge stored in a battery or power source due to a given amount of current over a certain period (in hours). We could also say amp-hours is the current an electric power source can discharge within one hour. Going by that, one amp-hour results from the discharge of one amp of current in one hour.
While watt-hours is a unit for measuring battery capacity, you will often find battery capacity written in amp-hours (Ah) on a battery pack.
Why Convert Watt-Hours to Amp-Hours?

When setting up an electrical system – such as a solar panel system – knowing the ideal ratings and sizes of the devices and units to use in the solar setup is essential. Making the wrong choices can lead to significant performance losses or even damage to the system.
Knowing the amp-hours of the power source used when setting up an electrical system can be pretty insightful. For one, it can help determine the type of fuse to use and the wire gauge.
To Determine the Ideal Wire Size
As evident in their current ratings, wire gauges are built to handle different loads. If battery capacity is in watt-hours, determining the amperage of an electrical system wouldn’t be so straightforward.
However, with amp-hours capacity, we can readily divide the amp-hours by the battery’s runtime to estimate the current going through the system. Once we know the current, we can easily choose the ideal wire size.
To Determine the Ideal Fuse Rating
As with choosing the ideal wire size, we need to know the amps of an electrical system to select the correct fuse since fuses are rated in amps.
With battery capacity in watt-hours, calculating the current going through the system wouldn’t be straightforward. But with the capacity in amp-hours, calculating current is easier.
Converting Watt-Hours to Amp-Hours (Wh to Ah) 
To calculate amp-hours from watt-hours, we’ll work with the formula for electrical energy and electrical power.
\(Electrical\ energy = power * time\ (1)\)
\(Power = voltage * current\ (2)\)
Rewriting (1) and (2) with the units of each quantity:
\(Wh = W * h\ (3)\)
\(W = V * A\ (4)\)
Substituting W for V x A in (3):
\(Wh = V * A * h\ (5)\)
Rewriting (5) to clearly show Ah:
\(Wh = V * Ah\)
Finally, to get the conversion, we’ll make Ah the subject of the equation by dividing both sides by V:
\(Ah = \displaystyle{\frac{Wh}{V}}\)
The conversion formula shows that to convert watt-hours to amp-hours, divide the value of watt-hours by battery voltage.
Example 1
How many amp-hours is stored in a 24 V battery if its watt-hours rating is 288 Wh?
The amp-hours of the battery:
\(\displaystyle{\frac{288}{24}} = 12\ Ah\)
Example 2 – Batteries in Series
If we have two 300 Wh, 12 V lead-acid batteries connected in series, what would be the overall amp-hour capacity of the battery bank formed from the connection?
This is not as straightforward as the first example since we have to figure out the average/total voltage of the series circuit.
In a series circuit, the voltage is equal to the sum of the voltage of the individual components. So, the voltage of the battery bank would be:
\(voltage\ V = 12 + 12 = 24\ V\)
Total Wh of the battery bank:
\(300 + 300 = 600\ Wh\)
Now that we know the voltage and watt-hours of the battery bank, we can convert watt-hours to amp-hours:
\(\small{amp\mbox{-}hour\ capacity\ of\ the\ battery\ bank = \displaystyle{\frac{600}{24}}}\)
\(= 25\ Ah\)
Example 3 – Batteries in Parallel
A solar power system uses a battery bank of three 12 V batteries connected in parallel. If the battery bank generates a total energy of 2500 Wh, what is its capacity in Ah?
Since the batteries are connected in parallel, they’ll experience the same voltage. Going by this, the voltage of the battery bank is 12 V.
Since the battery bank’s volts is 12 V, its capacity in Ah would be:
\(Ah = \displaystyle{\frac{2500}{12}} = 208\ Ah\)
Example 4
A 24 V lithium battery can discharge 30 watts of power for up to 8 hours. How much charge can the battery store (in amp-hours)?
To solve this, we’ll start by calculating watt-hours from the battery power and battery life:
\(Battery’s\ Wh = 30 * 8 = 240\ Wh\)
Next, we’ll convert watt-hours (Wh) to amp-hours (Ah):
\(the\ battery’s\ Ah = \displaystyle{\frac{240}{24}} = 10\ Ah\)
Another way to calculate the amp-hours of this battery would be to determine the battery’s amperage by dividing watts by volts. Then, multiply the amperage by the battery’s runtime.
Let’s determine the battery’s amperage:
\(Battery’s\ amperage = \displaystyle{\frac{30}{24}} = 1.25\ amps\)
The battery’s capacity in Ah:
\(Capacity\ in\ Ah = 1.25 * 8 = 10 Ah\)
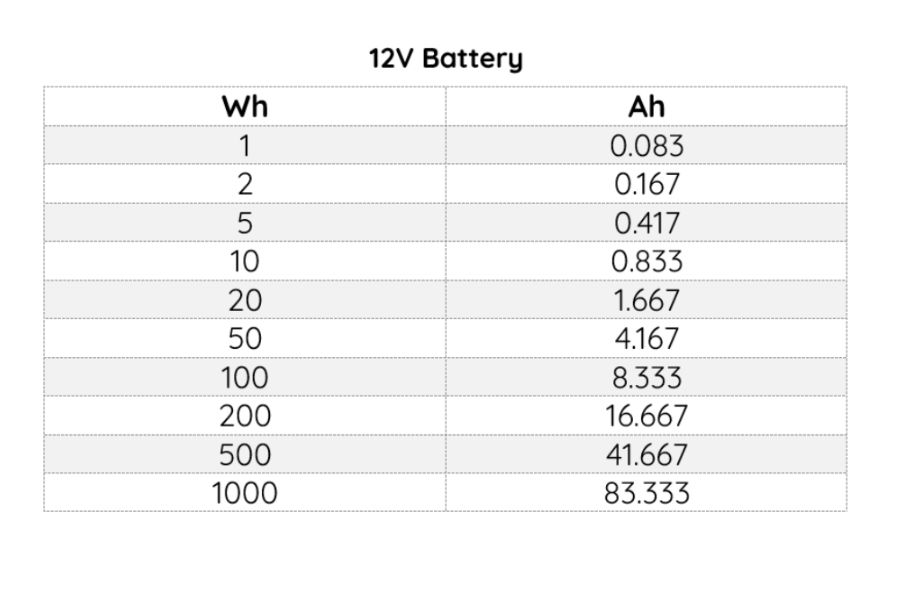
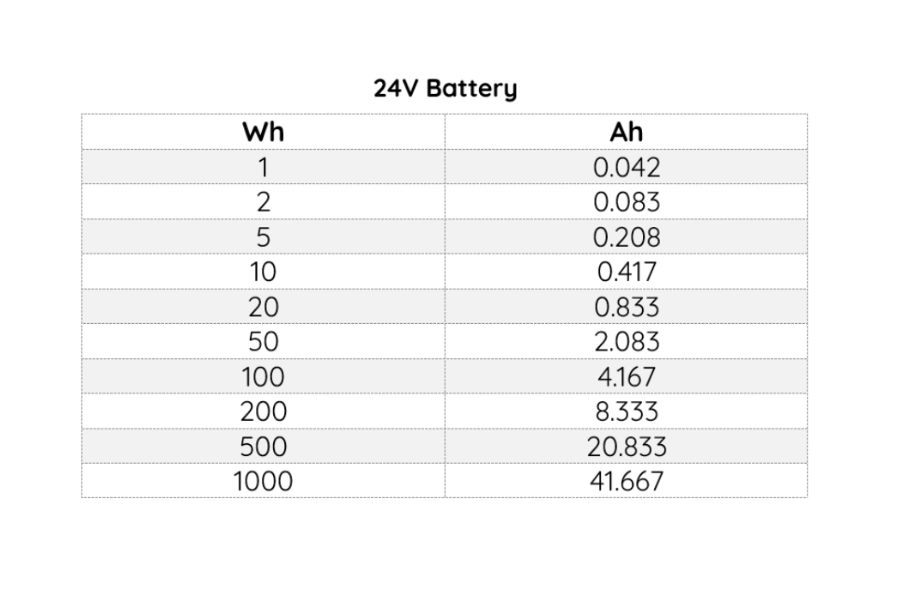
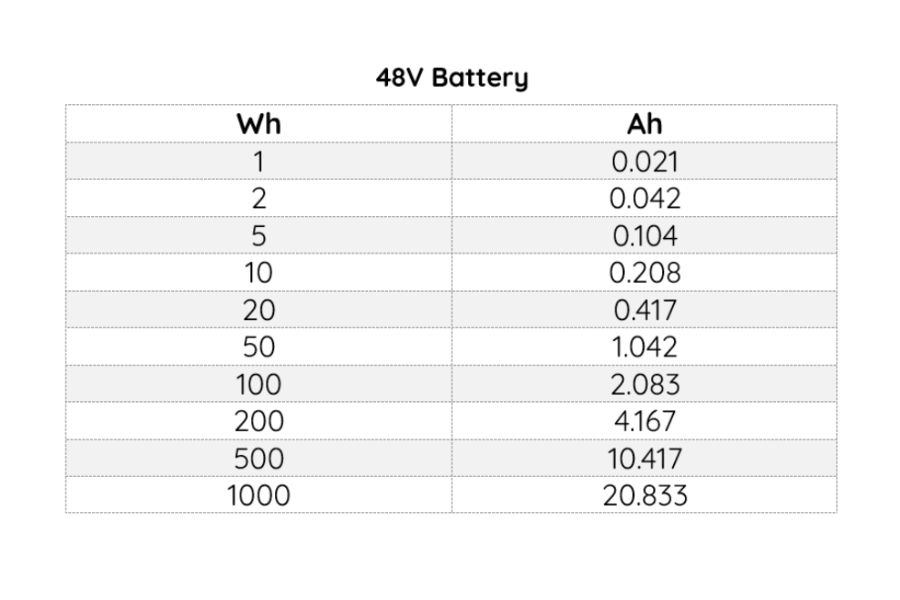
Watt-Hours to Amp-Hours Chart
How Do You Convert Amp-Hours to Watt-Hours?
The formula for converting amp-hours is pretty much an inverse of the watt-hours to amp-hours formula.
When converting watt-hours to amp-hours, we divide watt-hours by voltage:
\(Ah = \displaystyle{\frac{Wh}{V}}\)
But when converting amp-hours, we multiply amp-hours by voltage:
\(Wh =V * Ah \)
Examples
1. Let’s calculate watt-hours for a 24 V, 85 Ah car battery.
Going by the amp-hours to watt-hours conversion, this battery’s watt-hours would be:
\(24 * 85 = 2040\ Wh \)
2. How many watt-hours are stored in a battery bank of four 12 V, 48 Ah lithium batteries connected in series?
Since we’re dealing with multiple batteries connected, we cannot just do a direct amp-hours to watt-hours conversion. We must first determine the overall voltage and amperage of the circuit.
Since the batteries of the battery bank are in series, their total volts would be the sum of their volts:
\(\small{battery\ bank\ volts = 12 + 12 + 12 + 12 = 48\ volts}\)
In a series circuit, the average current throughout the circuit is the same. Going by that, the average Ah capacity of the battery bank would be 48 Ah.
Now that we know the overall voltage and amp-hours of the battery bank, we can do the amp-hours to watt-hours conversion:
\(48 * 48 = 2304\ Wh\)
3. If we have three 6 V, 10 Ah batteries in a parallel circuit, what would be the watt-hours of the circuit?
We cannot do a direct amp-hours to watt-hours conversion as with the previous example. We have to figure out the volts and amp-hours of the circuit first.
In a parallel circuit, the average volts are the same. So, the voltage of this circuit would be 6 V.
Amperage is summative in a parallel circuit. Therefore, amp-hours would also be summative. So, the amp-hours of this circuit would be:
\(10 + 10 + 10 = 30\ Ah\)
The watt-hours of the circuit:
\(6 * 30= 180\ Wh\)
How to Convert Kilowatt-Hours to Amp-Hours (kWh to Ah)
Kilowatt-hours is a unit of electricity use or production. It measures the energy produced or consumed from a given amount of power (in kilowatts) over a certain number of hours.
Like watt-hours (Wh) and amp-hours (Ah), kilowatt-hours can be used as the unit of a battery’s capacity. But what if we want to convert kilowatt-hours to amp-hours?
To show the conversion between kilowatt-hours (kWh) and amp-hours (Ah), we need two formulas:
- Watt-hours to amp-hours conversion:
\(Ah = \displaystyle{\frac{Wh}{V}}\ (1)\)
- Kilowatt-hours to watt-hours formula:
\(Wh = kWh * 1000\ (2)\)
Now that we have both formulas, we’ll substitute Wh for kWh x 1000 in (1):
\(Ah = \displaystyle{\frac{kWh * 1000}{V}}\)
So, to convert kilowatt-hours to amp-hours, multiply kilowatt-hours by 1000, then divide by voltage.